Background
Many times, we are interested in estimating the relationship between different variables that has a general form described as follows:
Where we do not have a specific function type defined (i.e., specific model):
As such, we would like to describe the data using the most appropriate model and estimate the parameters. In this introductory exercise, we will use nonparametric methods to do such a task and focus on three possible methods:
- Moving average = calculate the mean value, Y, around a window of X values
- Weighted moving averages = kernel smoothing: weight data as a function of distance, i.e., points closer in space are given greater weight
- Local polynomial regression: adjust the polynomial value based on least squares methods for observations in a local window (weighted by distance)
Packages
library(tidyverse)
library(Hmisc)
library(corrplot)
library(readr)
library(HH)
library(car)
library(scatterplot3d)
library(leaps)Data
For this example, we are using a database called Emissions. This data comes from FAO and represents the amount of emitted in different countries from Mexico to Panama. The number of years of data collection was 21. The data are also standardized based on the area under agricultural production. Given that one of the authors of this worked in Costa Rica, we will use that as our data source for the exercise. This will required working with a database that is in .csv format and then subset out the part that relates to Costa Rica. To accomplish this first part, we will using coding based on tidyverse, especially using dplyr.
Please note: I have located the data in my local Document folder for eash of reading this into R. You can change the location accordingly for your personal use. If you are using this as a script, you can also use the import options in RStudio.
emissions <- read_csv("Emissions.csv")
head(emissions)## # A tibble: 6 x 5
## Country Year Area CO2 CO2_area
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 Belize 1 128277 7.31 0.000057
## 2 Belize 2 153923 7.31 0.0000475
## 3 Belize 3 164124 7.31 0.0000445
## 4 Belize 4 184274 7.31 0.0000397
## 5 Belize 5 130610 5.85 0.0000448
## 6 Belize 6 173667 6.33 0.0000365# Quick summary of the results across the countries
summaries <- emissions %>% group_by(Country)
summaries %>% str()## Classes 'grouped_df', 'tbl_df', 'tbl' and 'data.frame': 168 obs. of 5 variables:
## $ Country : chr "Belize" "Belize" "Belize" "Belize" ...
## $ Year : num 1 2 3 4 5 6 7 8 9 10 ...
## $ Area : num 128277 153923 164124 184274 130610 ...
## $ CO2 : num 7.31 7.31 7.31 7.31 5.85 ...
## $ CO2_area: num 5.70e-05 4.75e-05 4.45e-05 3.97e-05 4.48e-05 3.65e-05 2.96e-05 3.36e-05 5.15e-05 5.60e-05 ...
## - attr(*, "spec")=
## .. cols(
## .. Country = col_character(),
## .. Year = col_double(),
## .. Area = col_double(),
## .. CO2 = col_double(),
## .. CO2_area = col_double()
## .. )
## - attr(*, "groups")=Classes 'tbl_df', 'tbl' and 'data.frame': 8 obs. of 2 variables:
## ..$ Country: chr "Belize" "CostaRica" "ElSalvador" "Guatemala" ...
## ..$ .rows :List of 8
## .. ..$ : int 1 2 3 4 5 6 7 8 9 10 ...
## .. ..$ : int 22 23 24 25 26 27 28 29 30 31 ...
## .. ..$ : int 43 44 45 46 47 48 49 50 51 52 ...
## .. ..$ : int 64 65 66 67 68 69 70 71 72 73 ...
## .. ..$ : int 85 86 87 88 89 90 91 92 93 94 ...
## .. ..$ : int 106 107 108 109 110 111 112 113 114 115 ...
## .. ..$ : int 127 128 129 130 131 132 133 134 135 136 ...
## .. ..$ : int 148 149 150 151 152 153 154 155 156 157 ...
## ..- attr(*, ".drop")= logi TRUEsummaries %>% summarise(
em_mean = mean(CO2_area),
em_sd = sd(CO2_area),
em_cv = sd(CO2_area)/mean(CO2_area)*100,
em_max = max(CO2_area),
em_min = min(CO2_area)
)## # A tibble: 8 x 6
## Country em_mean em_sd em_cv em_max em_min
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Belize 0.000106 0.000147 139. 0.000668 0.0000296
## 2 CostaRica 0.000415 0.000100 24.2 0.000649 0.000232
## 3 ElSalvador 0.000139 0.0000280 20.2 0.000196 0.0000983
## 4 Guatemala 0.000142 0.0000239 16.8 0.000172 0.000099
## 5 Honduras 0.000125 0.0000740 59.4 0.000281 0.0000224
## 6 Mexico 0.000111 0.0000147 13.3 0.000131 0.0000843
## 7 Nicaragua 0.0000614 0.0000182 29.6 0.0000923 0.0000242
## 8 Panama 0.000119 0.0000285 23.9 0.000169 0.0000828# Create a subset database to work with data only from Costa Rica
costa_rica <- filter(emissions, Country=="CostaRica")
head(costa_rica)## # A tibble: 6 x 5
## Country Year Area CO2 CO2_area
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 CostaRica 1 773395 271. 0.00035
## 2 CostaRica 2 783774 304. 0.000388
## 3 CostaRica 3 778918 317. 0.000407
## 4 CostaRica 4 740508 292. 0.000395
## 5 CostaRica 5 769340 341 0.000443
## 6 CostaRica 6 765005 341 0.000446Loess 1
This the method based on local polynomial regression.
# What does the relationship look like?
CR <- ggplot(data=costa_rica, aes(x=Year, y=CO2_area))
CR + geom_point()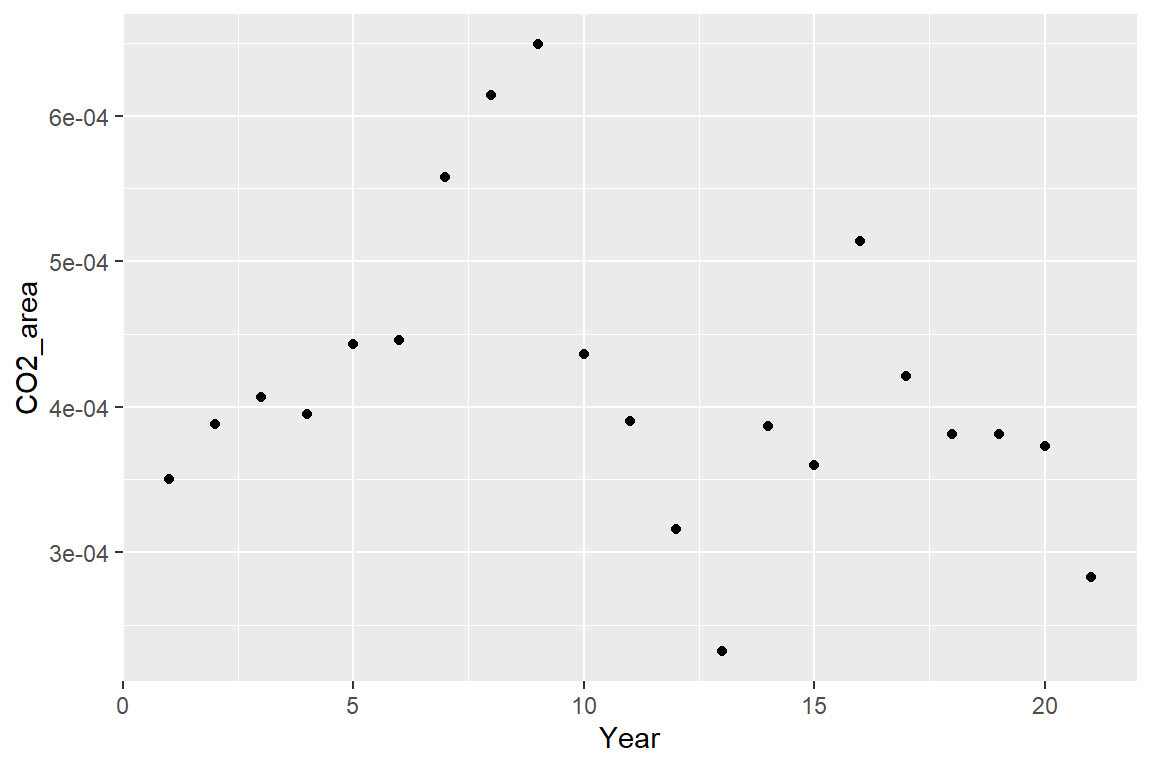
CR + geom_point() + geom_line()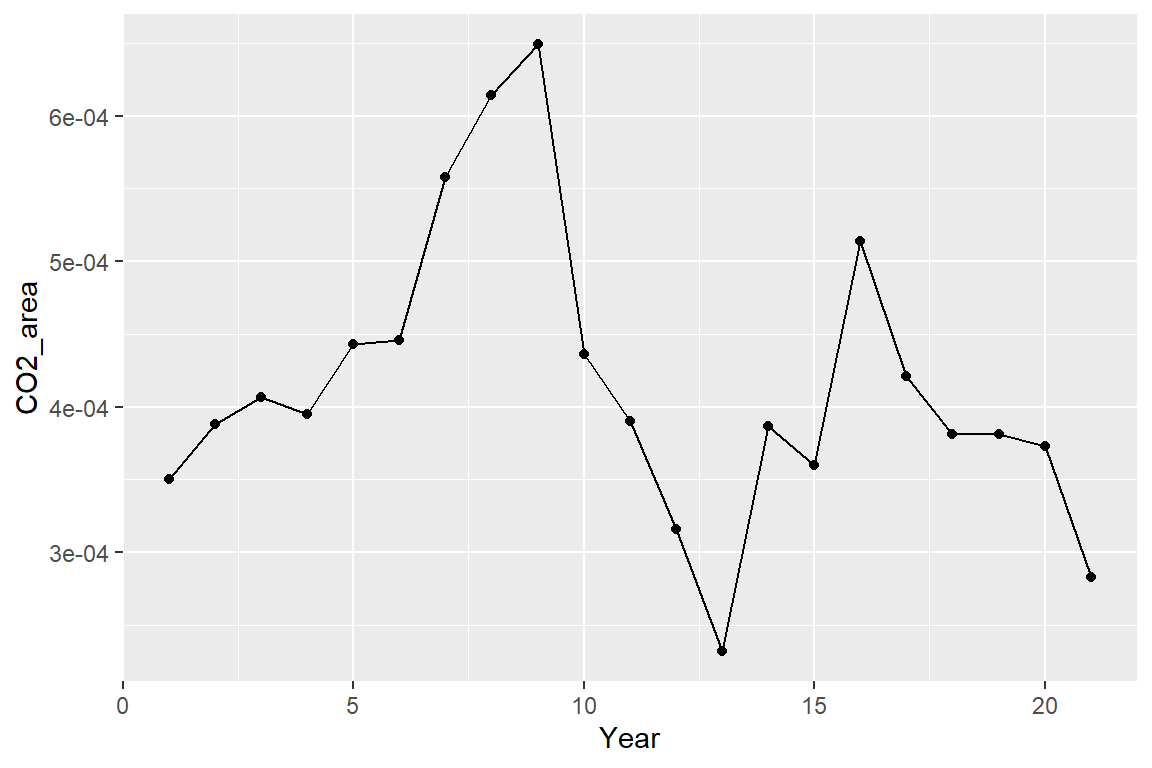
# Loess
cr_np1 <- with(costa_rica, loess(CO2_area ~ Year , span=0.75)) #default method
summary(cr_np1)## Call:
## loess(formula = CO2_area ~ Year, span = 0.75)
##
## Number of Observations: 21
## Equivalent Number of Parameters: 4.61
## Residual Standard Error: 7.132e-05
## Trace of smoother matrix: 5.06 (exact)
##
## Control settings:
## span : 0.75
## degree : 2
## family : gaussian
## surface : interpolate cell = 0.2
## normalize: TRUE
## parametric: FALSE
## drop.square: FALSEcrnp1_pred <- predict(cr_np1, data.frame(Year=seq(1,21,0.5)))
pred1 <- data.frame(Year=seq(1,21,0.5), crnp1_pred)
# Graphically
ej1 <- ggplot()
ej1 +
geom_point(data=costa_rica, aes(x=Year, y=CO2_area)) +
geom_line(data=costa_rica, aes(x=Year, y=CO2_area), lty=1) +
geom_line(data=pred1, aes(x=Year, y=crnp1_pred), lty=2)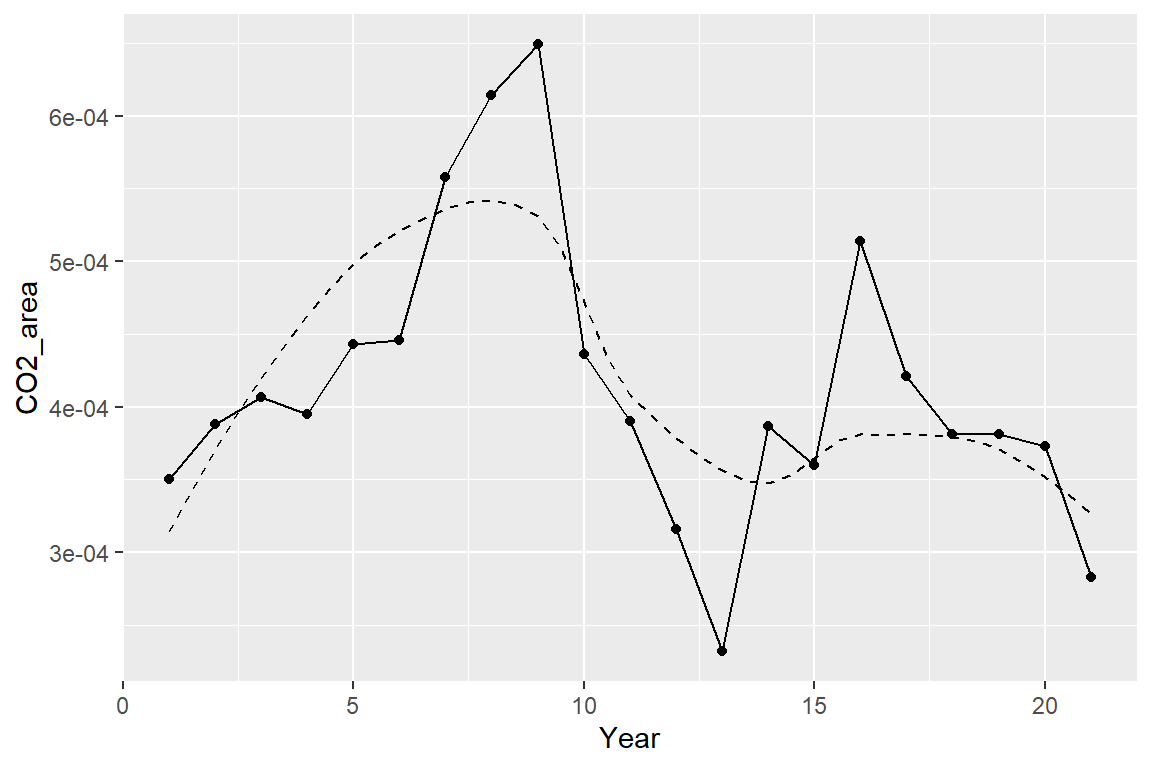
Modify the Loess line
Let’s look at some different line forms with Loess.
# Span=0.5
cr_np2 <- with(costa_rica, loess(CO2_area ~ Year , span=0.5))
crnp2_pred <- predict(cr_np2, data.frame(Year=seq(1,21,0.5)))
pred2 <- data.frame(Year=seq(1,21,0.5), crnp2_pred)
ej1 <- ggplot()
ej1 +
geom_point(data=costa_rica, aes(x=Year, y=CO2_area)) +
geom_line(data=costa_rica, aes(x=Year, y=CO2_area), lty=1) +
geom_line(data=pred1, aes(x=Year, y=crnp1_pred), lty=2, lwd=1.5) +
geom_line(data=pred2, aes(x=Year, y=crnp2_pred), lty=3, lwd=1.5)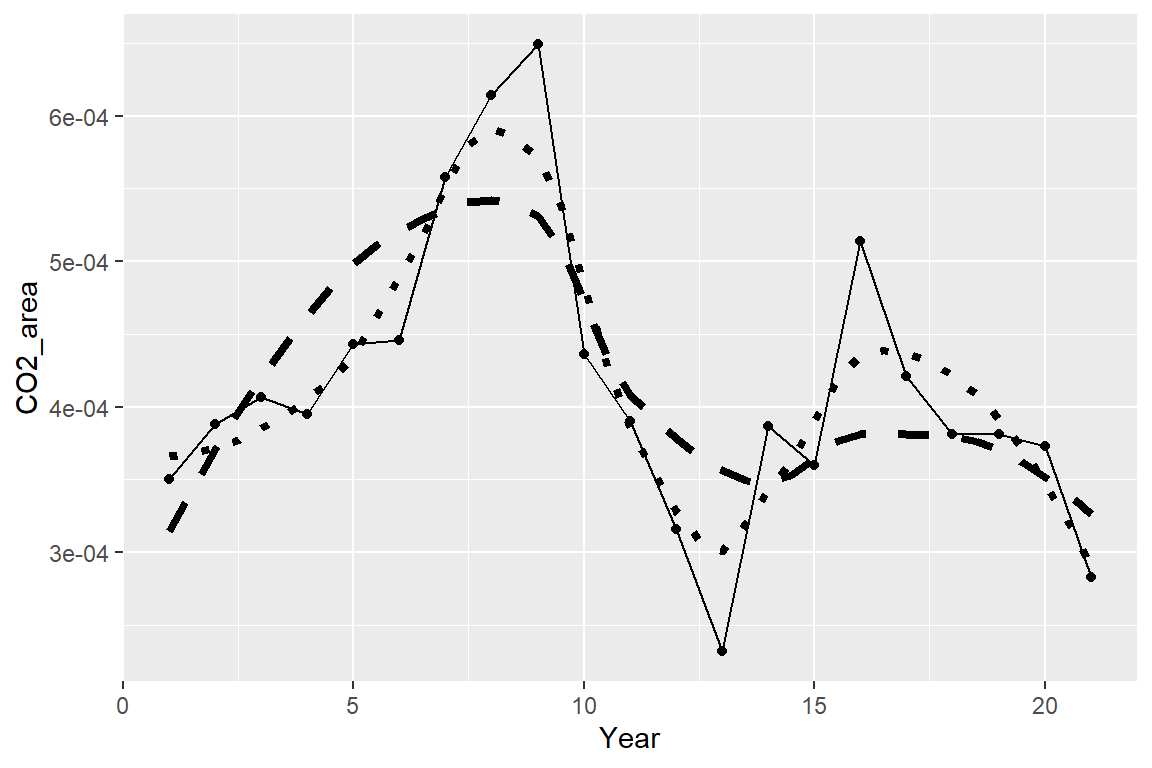
# Span=0.25
cr_np3 <- with(costa_rica, loess(CO2_area ~ Year, span=0.25))
crnp3_pred <- predict(cr_np3, data.frame(Year=seq(1,21,0.5)))
pred3 <- data.frame(Year=seq(1,21,0.5), crnp2_pred)
ej1 <- ggplot()
ej1 +
geom_point(data=costa_rica, aes(x=Year, y=CO2_area)) +
geom_line(data=costa_rica, aes(x=Year, y=CO2_area), lty=1) +
geom_line(data=pred1, aes(x=Year, y=crnp1_pred), lty=2, lwd=1.5) +
geom_line(data=pred2, aes(x=Year, y=crnp2_pred), lty=3, lwd=1.5) +
geom_line(data=pred3, aes(x=Year, y=crnp3_pred), lty=4, lwd=1.5)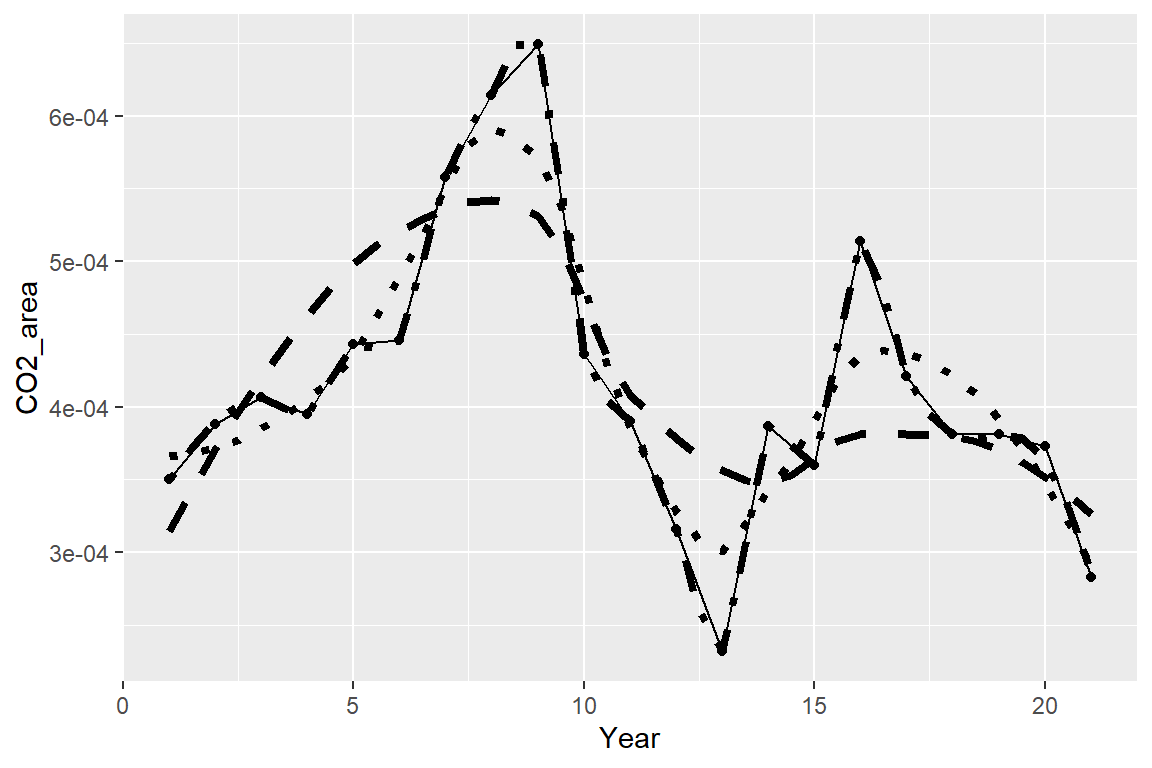
Smoothing splines
In our next example, we will use the function smooth.spline(). With this method, we can change the smoothing parameter and the methodology is based on crossed-validation to be able to define the parameter.
# Base method (by default)
cr_spline <- with(costa_rica, smooth.spline(x=Year, y=CO2_area))
cr_spline## Call:
## smooth.spline(x = Year, y = CO2_area)
##
## Smoothing Parameter spar= 0.3976519 lambda= 6.497957e-05 (11 iterations)
## Equivalent Degrees of Freedom (Df): 9.578523
## Penalized Criterion (RSS): 2.323599e-08
## GCV: 3.740554e-09summary(cr_spline)## Length Class Mode
## x 21 -none- numeric
## y 21 -none- numeric
## w 21 -none- numeric
## yin 21 -none- numeric
## tol 1 -none- numeric
## data 3 -none- list
## no.weights 1 -none- logical
## lev 21 -none- numeric
## cv.crit 1 -none- numeric
## pen.crit 1 -none- numeric
## crit 1 -none- numeric
## df 1 -none- numeric
## spar 1 -none- numeric
## ratio 1 -none- numeric
## lambda 1 -none- numeric
## iparms 5 -none- numeric
## auxM 0 -none- NULL
## fit 5 smooth.spline.fit list
## call 3 -none- callcrsp_pred <- predict(cr_spline, data.frame(Year=seq(1,21,0.5)))
pred4 <- data.frame(Year=seq(1,21,0.5), crsp_pred)
#Compare the fit with the Loess fit
ej1 <- ggplot()
ej1 +
geom_point(data=costa_rica, aes(x=Year, y=CO2_area)) +
geom_line(data=costa_rica, aes(x=Year, y=CO2_area), lty=1) +
geom_line(data=pred1, aes(x=Year, y=crnp1_pred), lty=2, lwd=1.5) +
geom_line(data=pred4, aes(x=Year, y=Year.2), lty=4, lwd=1.5)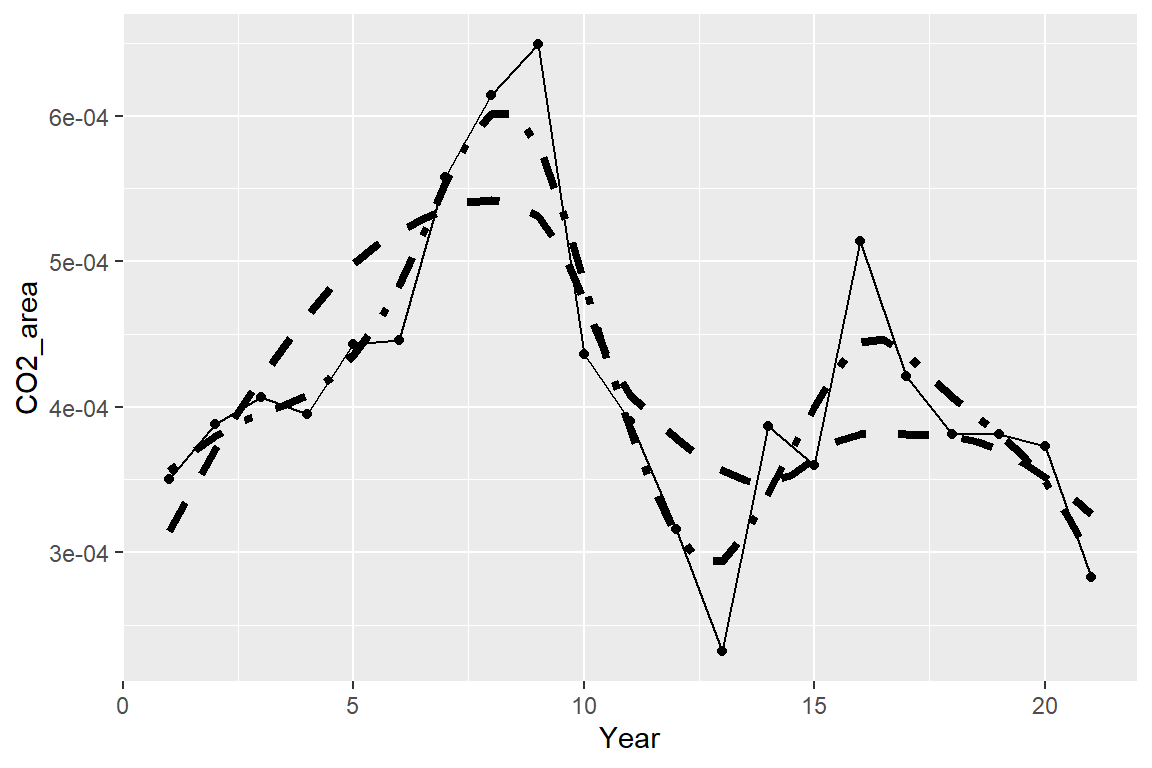
Change smoothing parameter
We will now create a series of model runs where we change the smoothing parameter.
cr25 <- with(costa_rica, smooth.spline(x=Year, y=CO2_area, spar=0.25))
pred25 <- data.frame(Year=seq(1,21,0.5), pred=(predict(cr25, data.frame(Year=seq(1,21,0.5)))))
cr35 <- with(costa_rica, smooth.spline(x=Year, y=CO2_area, spar=0.35))
pred35 <- data.frame(Year=seq(1,21,0.5), pred=(predict(cr35, data.frame(Year=seq(1,21,0.5)))))
cr45 <- with(costa_rica, smooth.spline(x=Year, y=CO2_area, spar=0.45))
pred45 <- data.frame(Year=seq(1,21,0.5), pred=(predict(cr45, data.frame(Year=seq(1,21,0.5)))))
cr55 <- with(costa_rica, smooth.spline(x=Year, y=CO2_area, spar=0.55))
pred55 <- data.frame(Year=seq(1,21,0.5), pred=(predict(cr55, data.frame(Year=seq(1,21,0.5)))))
cr65 <- with(costa_rica, smooth.spline(x=Year, y=CO2_area, spar=0.65))
pred65 <- data.frame(Year=seq(1,21,0.5), pred=(predict(cr65, data.frame(Year=seq(1,21,0.5)))))
cr75 <- with(costa_rica, smooth.spline(x=Year, y=CO2_area, spar=0.75))
pred75 <- data.frame(Year=seq(1,21,0.5), pred=(predict(cr75, data.frame(Year=seq(1,21,0.5)))))
cr85 <- with(costa_rica, smooth.spline(x=Year, y=CO2_area, spar=0.85))
pred85 <- data.frame(Year=seq(1,21,0.5), pred=(predict(cr85, data.frame(Year=seq(1,21,0.5)))))
ej1 <- ggplot()
ej1 +
geom_point(data=costa_rica, aes(x=Year, y=CO2_area)) +
geom_line(data=costa_rica, aes(x=Year, y=CO2_area), lty=1) +
geom_line(data=pred25, aes(x=Year, y=pred.Year.1), lty=2, lwd=1.2) +
geom_line(data=pred35, aes(x=Year, y=pred.Year.1), lty=3, lwd=1.2) +
geom_line(data=pred45, aes(x=Year, y=pred.Year.1), lty=4, lwd=1.2) +
geom_line(data=pred55, aes(x=Year, y=pred.Year.1), lty=5, lwd=1.2) +
geom_line(data=pred65, aes(x=Year, y=pred.Year.1), lty=6, lwd=1.2) +
geom_line(data=pred75, aes(x=Year, y=pred.Year.1), lty=2, lwd=1.3) +
geom_line(data=pred85, aes(x=Year, y=pred.Year.1), lty=3, lwd=1.3) 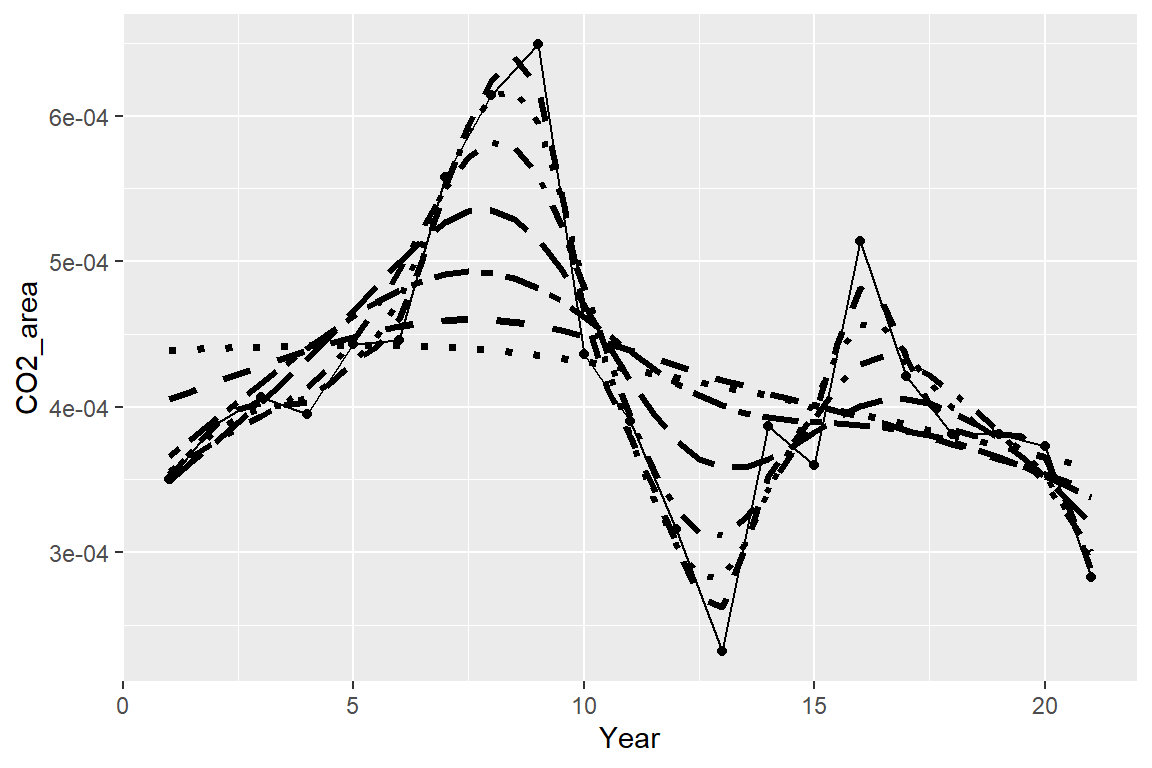
Last word for now
To close this discussion, it is natural to ask the following question, “What methods can we use to examine and control the smoothing parameter?”
Within this list, there are several including:
- trial and error,
- degree of smoothing compared with the data fidelity or reliability,
- minimize the mean square error,
- use cross-validation methods.